Leonid Frantsevich
Double rotation of the opening (closing) elytra
in beetles (Coleoptera).
Journal of Insect Physiology, 2012, 58: 24-34.
Abstract. Transient movements
of the elytra (opening and closing) were filmed in beetles tethered
from below. A total of 39 specimens of 18 species representing
11 families were examined. Bright markers glued to the elytra
were traced frame by frame. Body-fixed 3D traces of apical and
shoulder markers were reconstructed. Shapes of traces reflected
different steps of elytral movement and different types of flight.
Flat circular arcs were fitted to scattered traces using the least
square method. The rotation axis of the apical marker was always
directed at the contralateral side. The trace of the shoulder
marker was, as a rule, non-parallel to the apical trace. Usually,
the shoulder marker on the costal edge of the elytron uniformly
supinated in the course of adduction of the apical marker. Traces
of opening and closing coincided, hence the double rotation of
the elytron had one degree of freedom. The elytron to body articulation
in beetles is, presumably, a spherical mechanism with two separate
but linked drives for a broad swing during opening (closing).


(Movie) Tethered flight of Allomyrina
dichotoma with apical and shoulder markers.
Frame by frame positions of the
markers are expressed in the body-fixed coordinate system.
Position of the body-fixed system
in the insect body. Origin is at the apex of the scutellum. Axes:
transverse q, longitudinal p, dorso-ventral
v. Vector from the origin to an arbitrary point M is
described by projections of M on axes: mq, mp, mv respectively.
A beetle is Potosia aeruginosa with spreading wings.
(Movie) Tethered flight of Lucanus
cervus with apical and shoulder markers.
Reconstructed trace of apical markers
in Lucanus cervus in projection onto body-fixed planes:
equatorial q0p (small dots) and frontal q0v (big dots). Traces
of opening and closing coincide. Parts of the trace: initial elevation
and final depression (painted blue), broad opening-closing (red)
and flaps of the elytra induced by wing oscillations (yellow).
The trace of opening-closing is selected with the aid of linear
non-equalities (dotted lines).
Problem: fit a circle to a trace of opening-closing.
The trace is scattered in 3D space.
Fitting is acheved with a least square metod.
The problem is split in two steps.
First:
Construct a plane for which deviation of trace points from the
plane is minimal. 3D tilt of the plane is given by direction of
the normal onto this plane. Let us project all trace points onto
the normal. Their distribution on the normal is distribution of
deviations.
2D simplification of fitting
a line to the scattered trace (red dots)
 |
 |
(1) Projections of trace dots onto any one of parallell
lines are equally distributed. The same is true for 3D space.
Find the standard deviation σ for this ditribution. |
(2) Search for such direction of a straight
line where the value of σ is minimal (yellow group).
In 3D space this is the best fit of direction
of the normal for the plane of rotation. |
Thus the 3D problem is reduced to
1D. Now search for such direction of the normal with the given
azimuth φ and elevation ψ above the equatorial plane which yields
the minimal deviation. The best fit direction is direction of
the rotation axis of abduction-adduction (RAAM).
Map of the standard deviation σ
from the plane for the right apical trace in Lucanus cervus. RAAM
points at φ – 143?°, ψ - 49°.
Second.
Project all trace points onto the best fit plane and search for
position of the center of a circle inscribed into the trace. The
best fit center is a point which distances from projected trace
points provides the minimal scatter.

Map of the standard deviation σ from the
circle for the right apical trace in Lucanus cervus. The best
fit circular arc is inscribed into projections of trace points
(black dots). The center is indicated with the white dot.
The problem is solved.
Melolontha hippocastani:
projection d (in mm) of the apical trace P onto RAAM versus the
rotation angle ε (in ?°) does not depend on ε [green
dots], whereas projection of the shoulder trace Q increases upon
ε [red dots]. The shoulder marker Q supinates during opening
and pronates during closing.
Special cases of opening and closing
Traces of opening (hollow circles)
and closing (black circles) in Cybister laterimarginalis
are different. Top panel: projection onto the frontal plane; bottom
panel: projection onto the equatorial plane.
(Movie) Loop trajectory of the opening
and closing in Cybister laterimarginalis: elytra are
risen high (view the mirror image at the right), flap slowly,
then droop to the horizontal level and return to the closed position.
(Movie) Small opening of the elytra
and release of the wings through side incisions of the elytra
in a rose chafer Liocola lugubris.
(Movie) Small opening of the elytra
and release of the wings through side incisions of the elytra
in Scarabaeus sacer.
Search and flight postures in Scarabaeus
sacer in comparison with Egyptian images of a resting and
flying scarab. Top left: relief from the Karnak Temple in Luxor
(original photograph). Bottom right: Moon Pectoral (fragment;
Egyptian Museum in Kairo, JE 61884, Fund No 267 d). The flying
scarab was imaged with spread wings but completely closed elytra.
The phenomenon of double rotation
of the elytron is modelled with a flexagon or with a double guideways.
Leonid Frantsevich
Mechanisms modeling the double rotation of the
elytra in beetles (Coleoptera)
Journal of Bionic Engineering 2011, 8, 4: 395-405.
Abstract. We recorded transient
movements, i.e. opening and closing, of beetle elytra. The beetles
were tethered from below and filmed under a skew mirror; two markers
were glued on each elytron at the apex and at the base. Body-fixed
3D traces of the apical and basal markers were reconstructed.
The trace of the basal marker was, as a rule, non-parallel to
the apical trace. The costal edge of the elytron uniformly supinated
in the course of adduction of the apical marker. We found two
essential attributes of double rotation: (1) the elytron to body
articulation is approximately a spherical mechanism; (2) transient
opening and closing possess single degree of freedom. Moreover,
the double rotation was modeled with two mechanisms: (1) a flexagon
model of the Haas and Wootton’s type simulated the elytral movement
relative to the movement of one facet of the flexagon; (2) a screw
and nut model provided traces as two sectors of a helical thread,
one sector was phase shifted with respect to other one. Screw
guideways in a spherical mechanism give rise to discrepancies.
Exact solution for a spherical mechanism with two guideways was
proposed. The modeling revealed the attribute (3): the elytron
is actuated by two linked but differently directed drives. Experimental
investigations on the elytron to body articulation may be oriented
at search of those mechanisms.

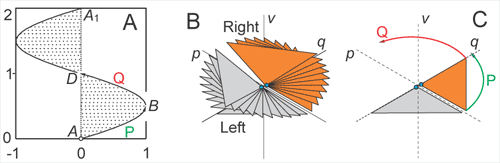
Flexagon model.
(A) Flexagon consists of four isosceles triangles with the common
apex and creases down the common legs. (B) Unfolding of a flexagon.
ζ is the dihedral angle between the (violet) stationary facet
AOD and the facet AOB which rotates about the crease AO. Facet
BOC (orange) is equivalent to the right elytron. OC is RAAM. (C)
Opening of a flexagon (stereopair). Only two facets are depicted:
the stationary facet AOD and the facet BOC, representing the right
elytron, which is shown in serial steps of opening. Adjust magnification
so that the distance between the centers of both figures would
be ~5.5 cm.
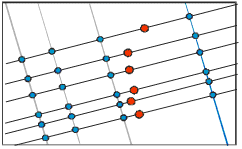
Helical opening of a model
elytron. (A) One wind of a basic right screw depicted
as a winding stairs, the lead and diameter equal 2. Axis of the
screw is AA1, AB ? trace of the apical marker P, BD - trace of
the shoulder marker Q. These model traces resemble real traces
in beetles. (B) Opening of model triangular elytra with simultaneous
supination; isometrical projection in the body-fixed space. Blue
dots - centers of rotation. Initial position of closed elytra
is depicted in (C). (C) Traces of the apical marker P and shoulder
marker Q of the right model elytron. They are the guiding reels
for the elytron. The reel model is a spherical mechanism.
|



